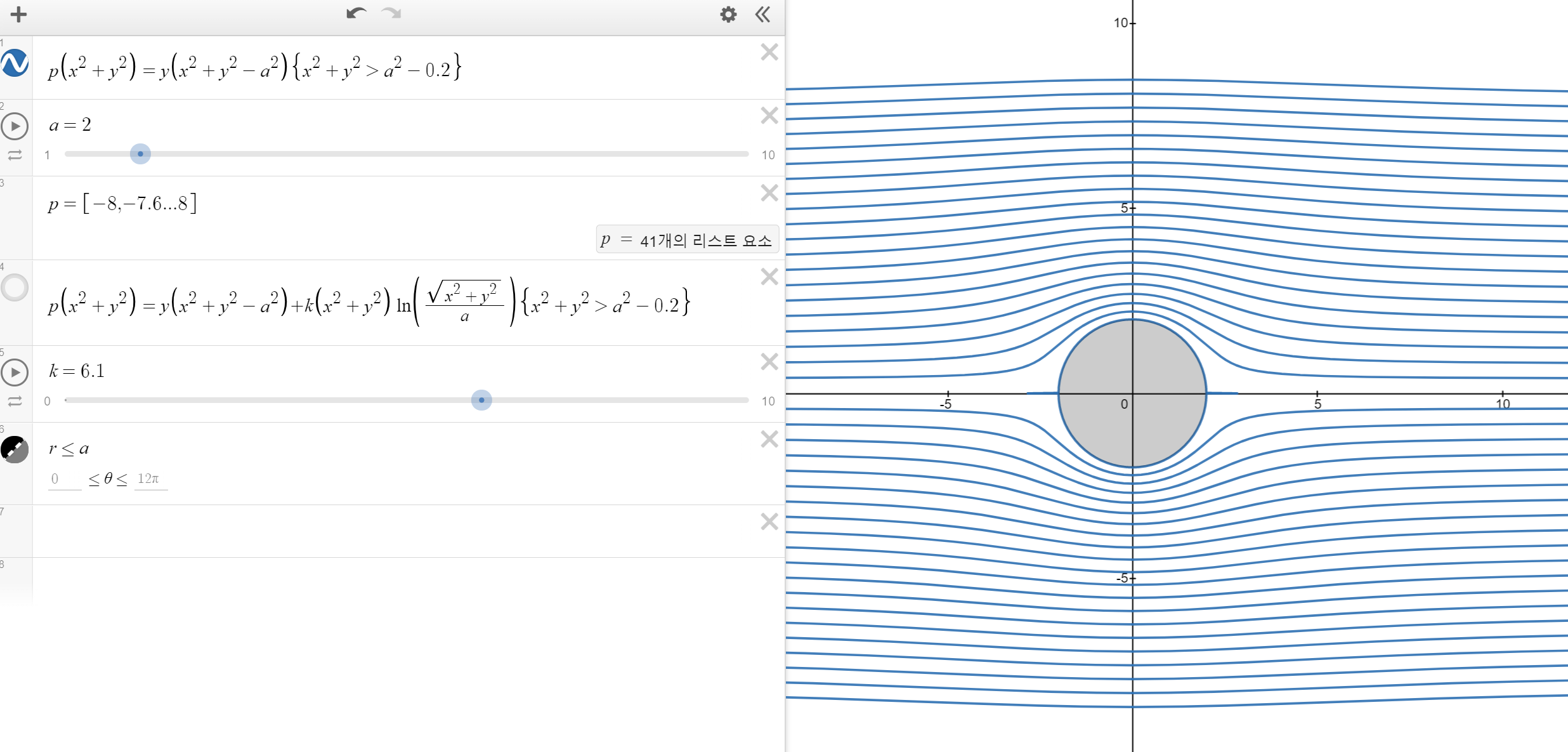
정지한 원형 장애물

시계방향으로 느리게 회전하는 원형 장애물
(통상 2개의 stagnation을 가지는데 회전이 빨라질때마다 서로 모이다가 하나로 응축된다
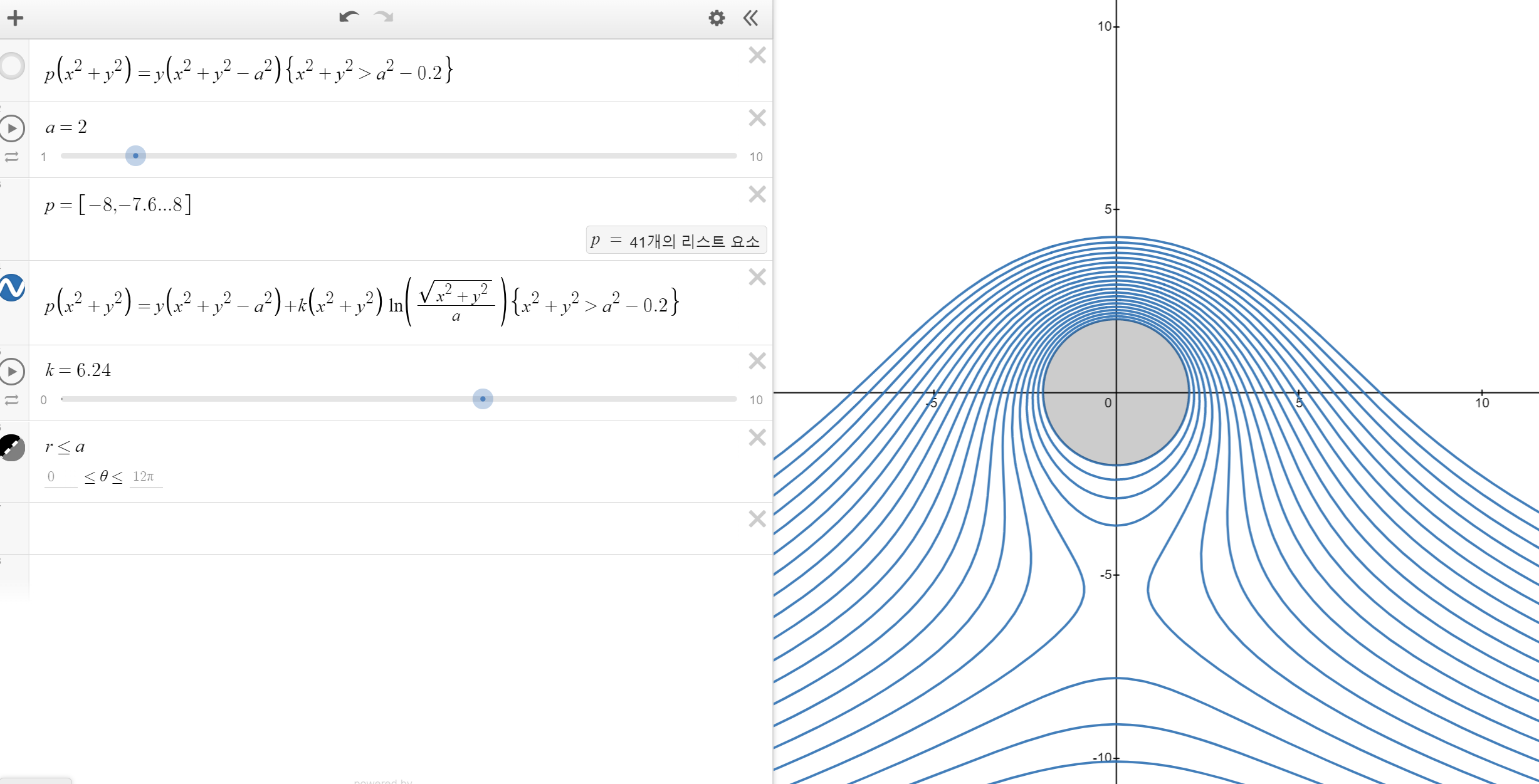
장애물이 더 빠르게 회전할 때 생기는 vortex
위의 모든 경우에서 drag가 0이 되는데 이것을 D'Alembert의 역설이라고 한다.
또한 lift는 먼곳의 유속 * 밀도 * 회전의 값으로 주어지는데 이것을 Kutta-Joukouski의 법칙이라고 한다
한편
Blasius의 적분법칙을 살폈다
drag와 lift를 압력 없이도(다시말해 베르누이 방정식을 풀지 않고도) 구할 수 있는 방법이다.
X - i Y = i * ρ/2 * complex velocity^2의 폐곡선적분
M = - ρ/2 * Real( z*complex velocity^2의 폐곡선적분 )
각각 1법칙 2법칙이라고 한다.
로랑급수와 유수정리를 대강 다시 보았다. (복소변수론을 먼저 훑으려고 했는데 어쩌다 보니 여기 진도가 더 빠르다)
오랜만에 1/(1+x^4)와 같은 것의 적분을 조금 해보았다
이후 conformal transformation을 살펴보았다.
z공간에서 까다로운 성질을 가지는 곡선을 사영변환하여 ζ공간에서는 간단한 성질을 가지도록 하는 것이다
두 공간에서 Laplace 방정식은 모두 만족할 수 있도록 해야한다
complex potential 또한 공유하도록 하는데, 한편 complex velocity는 퍼텐셜과의 미분관계를 생각할 때 항이 하나 더 붙는다
그럼에도 불구하고 U_inf와 그 각도 등의 성질, source, sink, vortex, doublet 등등 특이점의 강도 또한 그대로 유지되도록 한다.
의외로 쓸데없어보이긴 하는데 Joukowski transformation은 비행기 airfoil의 형태에 맞게 적절한 변환을 제공한다.
z = ζ + c^2/ζ의 꼴로 변환관계에 있다.
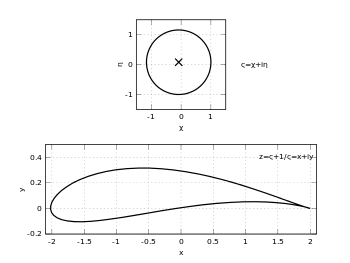
대충 비행기 airfoil 모양스러운 변환.
당분간 저 내용이 나올 것 같은데
비행기 날개에서 흐르는 공기 모형같은건 ㅈ도 관심 없으니까 내일부터 이쪽은 건너뛰고 봐야겠다
것보다 유체로 하는 수치해석 기법 어디서 배우지?
'[硏 Ⅰ] 연구하다 - 교양 > 시험 공부 전반' 카테고리의 다른 글
| 전반적인 고교 내신 시험 공부법 (글 미완성) (0) | 2021.12.11 |
|---|---|
| 2021년 1학기 신화 발표 슬라이드 (0) | 2021.09.27 |
| 9/23 상담학 (0) | 2021.09.23 |
| 유체 (0) | 2021.09.15 |
| 핵융합 이론 정리 (3/4) (0) | 2021.08.15 |


댓글