[검색해서 들어오신 분들께 : 이 글은 정보가 없습니다!]
갑자기 삘받아서 듣고 있는 핵융합
그냥 어떤 내용들이 있는지만 궁금해서 수식은 자세히 살피기보다는 가볍게 정리

오늘은 핵융합 를! 할거예요.
Nuclear Fusion Fusion Reactions
태양과 별의 에너지원 : 핵융합. Nuclear Fusion.
1905년에 아인슈타인의 E=mc^2가 발표된 이후...
D+T -> alpha + n + 17.6MeV
반응물의 질량이 더 크다. 여기에서 빠져나간 질량이(질량결손) 뒤에 해당하는 에너지.
욕조에 바닷물을 채우고 노트북 리튬 배터리로 핵융합 반응을 시키면 200MW
-> 한 사람이 50년정도 쓸 수 있는 에너지.
구현의 어려운 점 : 뜨거운 태양을 어떻게 가둘 수 있는가?
태양은 중심부 온도가 1~2억도가 넘는다. 이것을 어떻게 지구에서 구현하는가?
바깥으로 나가려는 힘 : ΔP(그래디언트)
안으로 가두는 힘 :
- g(중력)의 경우 중력가둠.
- 레이저 등을 이용할 경우 관성가둠.
- 자기장을 이용해 가두는 경우 자장가둠. 토카막.
태양은 플라즈마의 상태로 되어있다. 전자와 핵이 구속되어있지 않고 떨어진 상태. 따라서 자기장을 이용할 수 있다.
어떻게 온도를 높이는가?
- Ohmic heating : 플라즈마 내에 전류가 흐르면 저항이 흐른다.
- NBI : 중성입자를 주사하여 에너지를 준다.
- RF : 공명을 이용하여 에너지를 준다.
에너지를 전기로 어떻게 옮기는가?
- 플라즈마가 중심에 있으면 바깥에 blanket.
- 리튬(3중수소 근원)을 그곳에 집어넣는다
=> DT반응을 통해 alpha와 n이 나온다.
alpha는 가두어지는데 n은 blanket 바깥으로 나오게 된다.
- n은 에너지가 14.1MeV로 매우 높은데, 플라즈마 주변에 냉각재를 흘려보낸다. 여기에서 열을 얻어 터빈을 돌린다.
현황?
- KSTAR : 2007년부터 연구중
- ITER 프랑스 : 2025년 완공
문제점
- 플라즈마의 turbulance 현상
- 불안정성으로 인해 구조가 달라지는 것
- 플라즈마에서 나온 중성자가 플라즈마 재료와 부딪히면 방사화된다. => 재료 선정의 문제
- heat flux를 견뎌내는 문제 => 재료의 문제

물질 <-> 에너지
- E = mc^2
- binding energy와 Z : 철에서 극대점인 형태의 그래프
- n과 p가 합쳐지기 전과 후를 비교했을 때 줄어드는 에너지를 binding energy라고 한다.
- Fe보다 가벼운 것들이 Fe로 가는 과정은 핵융합
- Fe보다 무거운 것들이 Fe로 가는 과정은 핵분열

p-p chain (온도가 낮은 별)
p + p -> d
d + p -> He(3)
He(3) + He(3) -> alpha(He)
- 태양에서는 p-p chain으로 초당 3.8E26J의 에너지를 낸다. 질량은 4.3E9kg이다. p가 73%이며 He가 25%이다.
=> 태양의 나이와 남은 수명을 유추할 수 있다.
보다 온도가 높은 경우 CNO cycle
- 4p -> alpha
보다 더 온도가 높은 경우 triple alpha
alpha + alpha -> Be
Be + alpha -> C
p와 p가 밀어내는 힘 : Coulomb힘.
- 극복하려면 0.4MeV가 필요. 40억도 정도가 필요.
- 물론 온도가 더 낮더라도 양자 터널링 현상에 의해 가능.
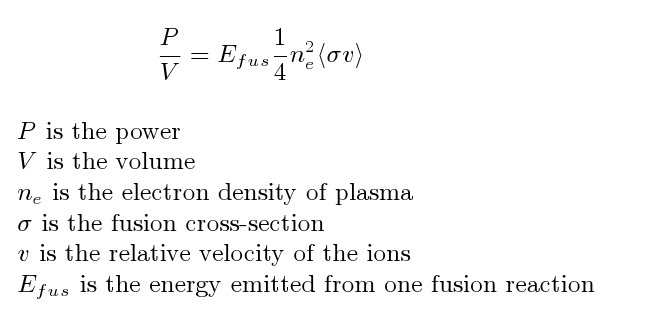
fusion power
= N(밀도)a * Nb * (두 계가 핵융합을 일으킬 수 있는 cross-section * 둘의 상대속도) * 반응을 한번 할 때 발생하는 에너지
- R_fu(fusion reaction rate 밀도)는 어떻게 식이 얻어지는 것일까?
아시모비치 : 토카막 최초 개발자.
- 언제 핵융합 발전소를 만들 것인가요?
=> 사회가 필요할 때 만들어질 것입니다. => 언제일까? ㅋㅋ
- 우리나라는 2040년, 2050년에 DEMO 토카막이 돌아갈 예정. 물론 바뀔 수는 있다...
Fusion Fuels, Thermonuclear Fusion
- 어떤 핵융합 연료를 사용할 것인가? 그리고 어떻게 지구에서 구현할 것인가?
1. d + t -> alpha + n
2. d + d -> t + p 또는 He3 + n
3. d + He3 -> alpha + p
- 순서대로 1, 2, 3세대
중요한 조건 : abundancy. cross section.
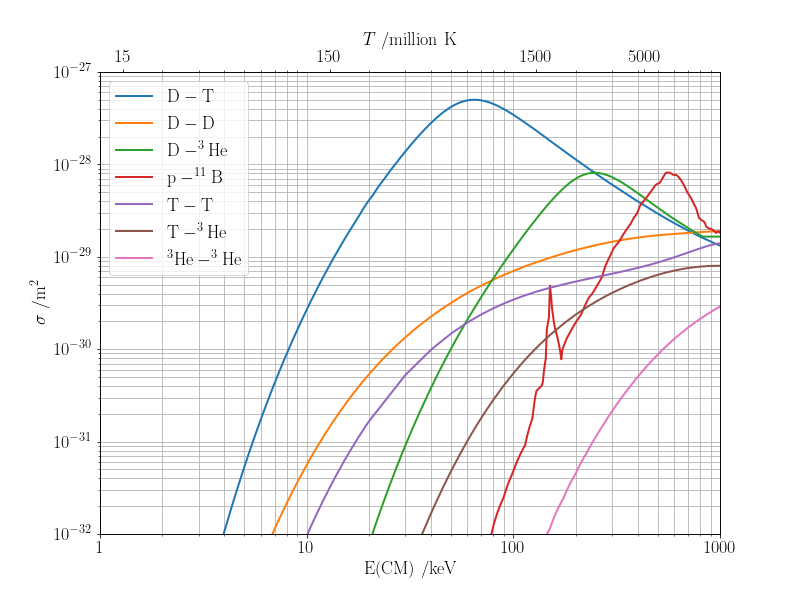
1세대 d-t를 선택 : 온도가 낮아도 괜찮고 cross section이 상당히 낮다
- d는 지구에서 매우 쉽게 구할 수 있다.
- 다만 t는 구하기 어렵고, 반감기도 12.3년이다. 지구 전체에 50kg쯤 있지 않을까. 중수로의 D2O가 중성자를 잡아먹으면 T가 만들어지기도 한다.
- n이 냉각수에 부딪혀서 나온 열에너지로 터빈을 돌린다. (30% 효율)
- n + Li -> t : 토카막에서 나온 중성자가 바깥 층의 리튬과 반응하면 삼중수소가 만들어진다. 이것을 계속 토카막에 넣으면 반응을 유지할 수 있지 않을까?
- 참고 : Li6은 4.78MeV를 내놓는 반응이며 전체 리튬의 7.42%를 차지한다. Li7은 중성자를 또 다시 내놓는 장점이 있지만 -2.47MeV를 내놓는 흡열반응이다...
=> blanket을 설계할 때 Li6과 Li7을 각각 어디에 두어야 최적일까?
2세대 d-d를 선택 : d + t, d + He3, t + He3, t+t, He3+He3 등의 side 반응들이 존재한다.
3세대 d-He3을 선택 : t -> He3 + beta 반응. He3는 달에 매우 많이 발견된다.
- He3으로 direct conversion을 어떻게 하는가?
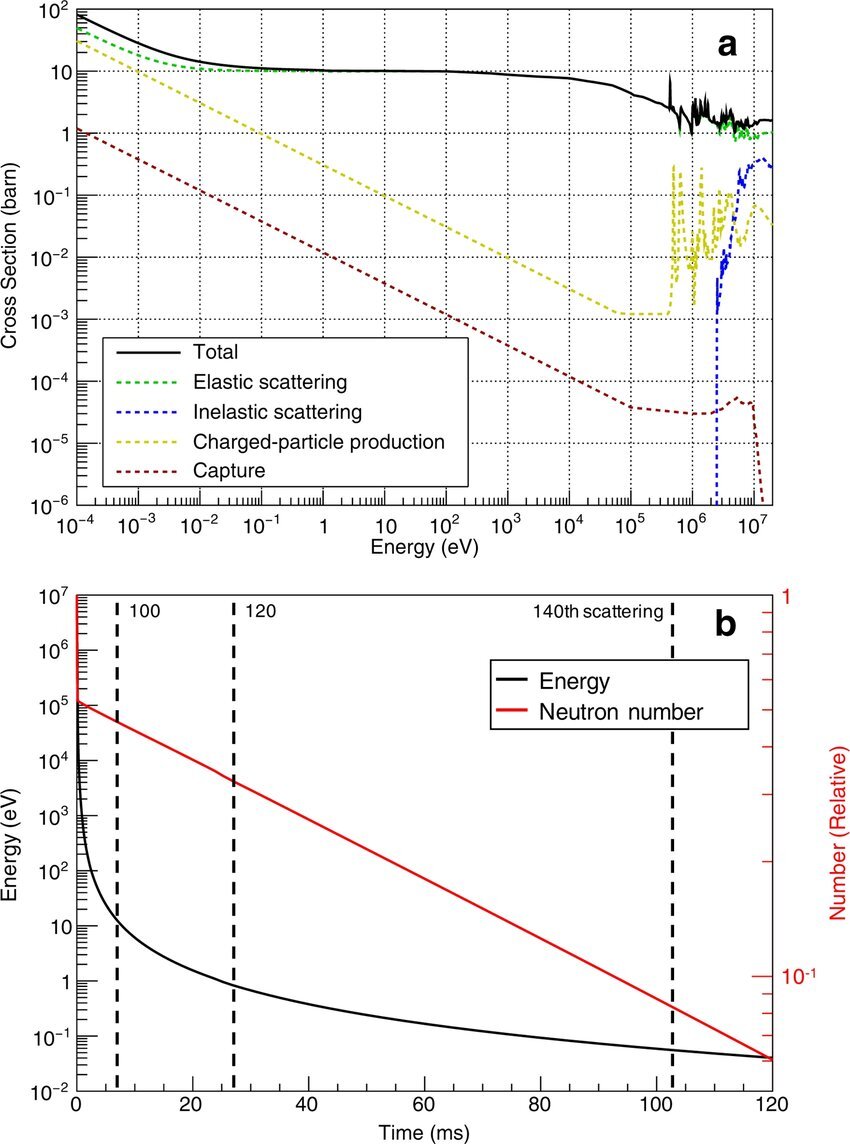
d + t -> alpha + n ( d를 t의 beam에 주사한다)
=> T-cross section 그래프를 볼 때 기존의 것보다 100배 이상 cross section이 높다.
- 이것을 Thermonuclear fusion이라고 한다.
- 남자들과 여자들을 강제로 가두면 언젠가는 커플이 생기지 않을까? (confinement)
Fusion energy는 clean energy인가?
- d-He3 반응은 반응 생성물에 n도 없고 t도 없어서 방사성 물질이 없어 깨끗할...?까?
Fusion을 어떻게 가능하게 하는가?
- beam을 서로 쏘아 부딪히게 하는가? beam을 다른 물체에 부딪히는가? 토카막?
- 혹은 다른 아이디어는?
Fusion Reactor Energetics
- 핵융합로는 어떤 조건을 만족해야 할 것인가?
난로 안에 에너지원으로 토카막을 둘 때...
- 난로가 돌아가려면 연료가 필요할 것이다(t, d, He3 등)
- 더 많은 연료를 넣으면 더 따뜻해진다 : density(n = #[m^-3])
- 온도가 높으면 더 많은 에너지 : [KeV]
- confinement time, insulation, 얼마나 더 오래 가둘 수 있을 것인가 : tau [s]
Lawson : n * tau * T > ??일 때 가능하다
reactor에 쓰이는 E out이 E in보다 커야만 한다. (당연하다)
- E out = E_fu + E_aux(auxilliary heat플라즈마를 뜨겁게 만들어서 핵융합이 일어나게끔 하는)
- E in = E_n(빠져나가는 n) + E_rad + conduction(=int 0 to tau_b E_th/tau_E)
- tau_E = Energy confinement time
- reactor에서 잃어버리는 에너지만큼은 넣어주어야 한다.
Q_p = E_fu/E_aux
- Energy amplification factor
Ignition condition
- Q_p -> infty (외부에서 플라즈마를 뜨겁게 만들어주지 않아도 핵융합이 유지되는 상황)
Breakeven condition
- Q_p=1 (얻는 것과 넣는 것이 같다...)
- 다만 실용적으로는 20~30정도의 Q_p가 있어야 할 것이다.
Fusion reactor의 필요조건
- D, T를 연료로 하고 n, tau, T를 고려
- fusion triple product가 역치를 넘어야 반응이 된다면, 그 값을 어떻게 높일 수 있을까?
- 세 값을 모두 높일 필요는 없을 것이다.
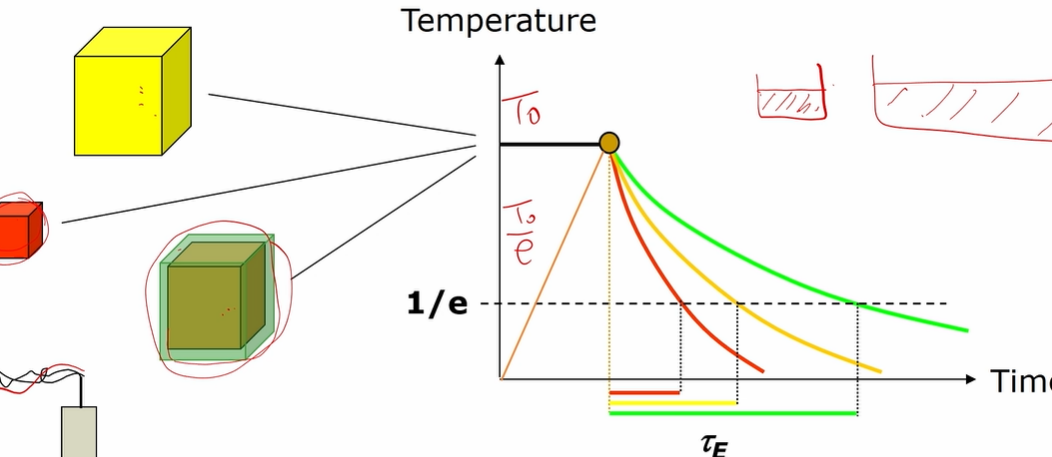
Energy confinement time
- beam을 서로 쏘아 충돌시키는 scattering cross section은 fusion의 값보다 훨씬 크다.
- 그렇게 얼마나 입자를 잘 가두는지를 confinement라고 한다.
- tau_E는 시간에 따라 Temperature을 그릴 때 원래 T에서 1/e만큼 떨어질 때까지의 시간.
- tau_E가 크다면 열손실이 최소이다. 장치가 크고 단열이 잘 될수록 이 값이 커진다.
- particle confinement time, momentum confinement time은 무엇?
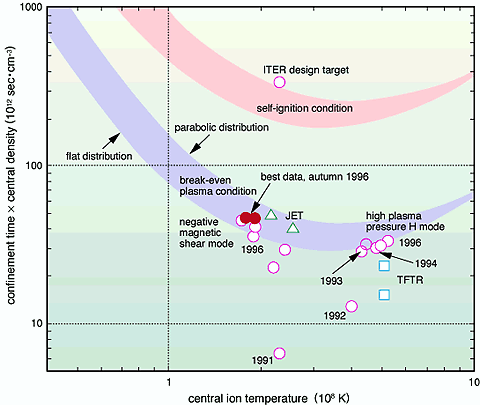
- n*tau - T의 그래프는 대개 포물선의 형태이다
- Q_p = E_fu/E_aux = E_fu/(eta_in * E_in)
- 현재까지의 기록 : 1997년 JET에서 p_fu=16MW, Q=0.64 (D-T)
- 최근의 JT-60은 Q=1.25, JET은 Q=1.14가 나왔다. (d-d를 d-t로 환산)
=> 물론 이것은 D-D의 값을 D-T로 환산한 값이다. (d-t는 방사성 물질의 걱정이 있다)
- 이 값은 어떻게 환산되는 것인가?

- dt의 경우 p_fu는 Nd * Nt * <sigma*v>_dt * Q_fu,dt
- dd의 경우 Nd^2 * <sigma*v>_dd * Q_fu,dd /2
=> 이 값으로 환산가능?
Fusion multiplication factor는 충분한 개념인가?
Single Particle Approach
- 플라즈마의 기술. 지배방정식.
- single particle approach, kinetic approach, fluid approach의 3가지 방법론이 있다.
=> 왜 저 3가지만 고려하는가? 같이 쓰면 안되는가?
- F = ma = mv' = g(E + v cross B) : 지배방정식
- v는 x,y,z의 t에 대한 값으로 나타난다.
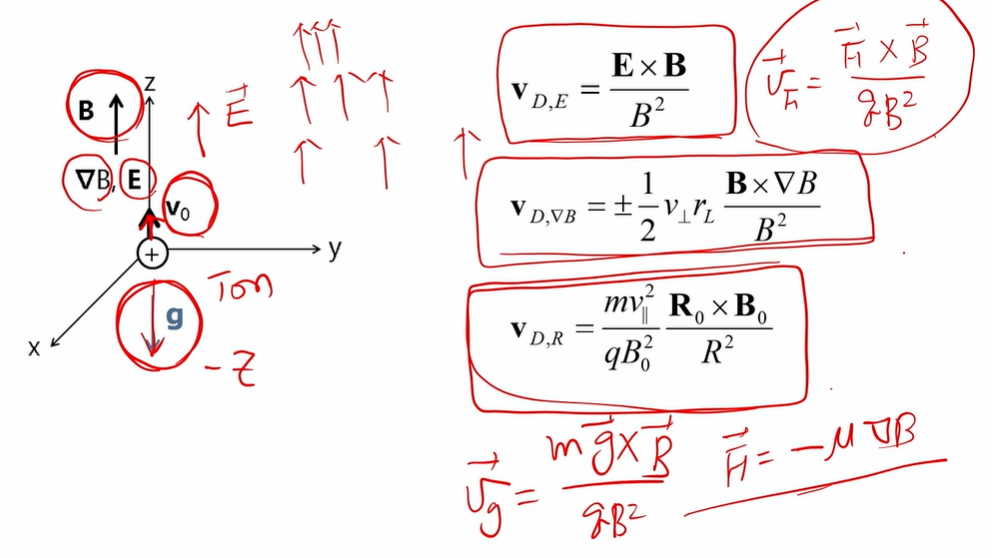
- 일반적으로 F에 대해 drift motion이 나타난다면 : v_F = F cross B / (q * B^2)
1. B=0, E가 있다 : E의 방향으로 가속.
2. E=0, B가 있다 : B를 축으로 도는 원운동. (방향은 자기력 방향 고려) mv/Bq가 반지름.
3. E, B가 모두 일정 : drift motion.
- v_E = E cross B / B^2
4. grad B (B가 불균일) : drift motion
- v_gradB = 1/2 * r_L * r_perpendicular * (B cross gradB) / B^2
5. 자기장의 curvature : drift motion, 곡률반경 R
- v_R = m * v_parallel^2 * R cross B / (q * B^2 * R^2)
-입자가 움직이는 방향에 gradB가 있는 경우 -mu*gradB의 힘을 받는다. (mu = -1/2 * m * v_L^2 / B. 시간보존량)
- 지구 북극은 S극이고 남극은 N극이다.
- 태양풍의 플라즈마가 지구로 날아오는데 지구 자기장에 의해 보호받는다.
=> 태양풍 ion 입자는 어떻게 움직이는가?
=> 오로라는 어떻게 극지방에 나타나는가?
- 토카막 속의 이온 입자의 움직임은 어떻게 되는 것인가?
Kinetic, Fluid Approach
Kinetic approach : f(t,x,y,z,vx,vy,vz)

- 볼츠만 방정식 : df/dt = partial df/dt + v circle grad f + g/m*(E + v cross B) circle grad_v f
- x,v쌍의 6차원 상공간으로 표현된다.
- 왜 f의 전미분이 저렇게 표현되는가? : 수학적, 물리적 의미를 생각해보기...
- 전미분의 값이 0일 때 : Vlasov equation
- 전미분의 값이 (f_n - f)/tau일 때(tau는 n과의 collision time) : Krook collision term
- 이것들은 각각 어떤 의미를 가지는지?

- 맥스웰 방정식 : eta0 div E = sigma, div B = 0, curl E = - round dB/dt, curl B = mu0*j + mu0 * eta0 * partial dE/dt
Fluid approach
- 여전히 위에서 다룬 변수들을 얻는것은 어려운데, n, v, T, P 등의 쉬운 변수로 나타낼 수 있으면 플라즈마를 더 쉽게 이해할 수 있지 않을까?
=> 위의 kinetic approach를 속도 v에 대해 모두 적분한다.
=> 연속방정식, 운동량 보존 방정식, 에너지 보존 방정식.


- Two fluid equation : ion과 e의 n, v, T를 다루는 것.
- Single fluid equation : MHD(magnetohydrodynamic) equation, 위의 두 방정식을 합친 것.
- ideal MHD equation : resistive=0의 가정. 가장 단순.
=> 이런 모델로도 equilibrium, stability 등을 따지기 좋다

Kinetic approach가 필요한 이유는?
- KSTAR의 경우 전자밀도는 10E20m-3. 체적은 18m3.
=> # of electrons는 약 10E21...
=> 이거 과연 single particle approach가 가능할 것인가? ㅋㅋ
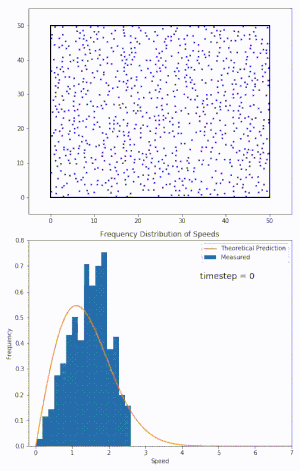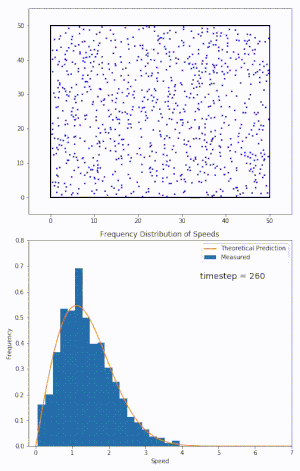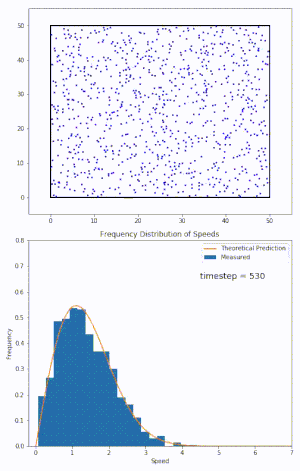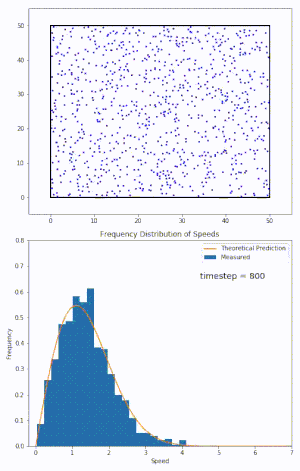
Maxwell distribution
- 입자 system이 열평형상태에 도달하게 될 때 maxwellian velocity distribution을 띠게 된다.
Plasma Equilibrium, Stability, and Transport
- 풍선을 불어놓고 정지한 상태 : equilibrium
- 나가려는 힘 : grad P force
- 누르는 힘 : 고무의 tension
=> 두 힘이 균형을 이루는 상태. force balanced.
- 플라스마도 나가려고 하면 잡아주는 것이 중요하다.
- 평형이 중요한 것이 아니라 안정평형이 중요하다...
- stability의 중요성.
- 플라즈마도 너무 크게 용기를 만들면 불안정할 수 있다.
- transport : grad n, grad T에 의해 퍼져나가는 현상.
Equilibrium
- 간단한 가정의 지배방정식 :
1. J cross B = grad P (모멘텀 방정식)
2. curl B = mu0 * J (암페어 법칙)
3. div B = 0 (자기입자가 존재하지 않음)
Stability
- Q1 : 살짝 건드려주는 값. 위치와 시간에 대한 함수. = Q(r) * exp{ -i * (wr + i * wi) * t }
- wi가 양수인지 음수인지가 관심사. (진폭이 커지는가=시스템이 붕괴=불안정, 작아지는가=안정)

Transport
- J = -D * grad n (Fick's law, 농도가 높은 곳에서 낮은 곳으로 flux가 생긴다)
- q = -K * grad T (Fourier's law, 온도가 높은 곳에서 낮은 곳으로 flux가 생긴다)
- grad를 없애는 방향으로 flux는 만들어진다.
MHD equations :
- equilibrium에서 v=0으로 정적이다.
- ideal의 경우 : Force balance(grad p = J cross B), Ampere's law, Closed magnetic field lines
- 만약 v가 0이 아닐 때는...? : 식이 좀 달라진다
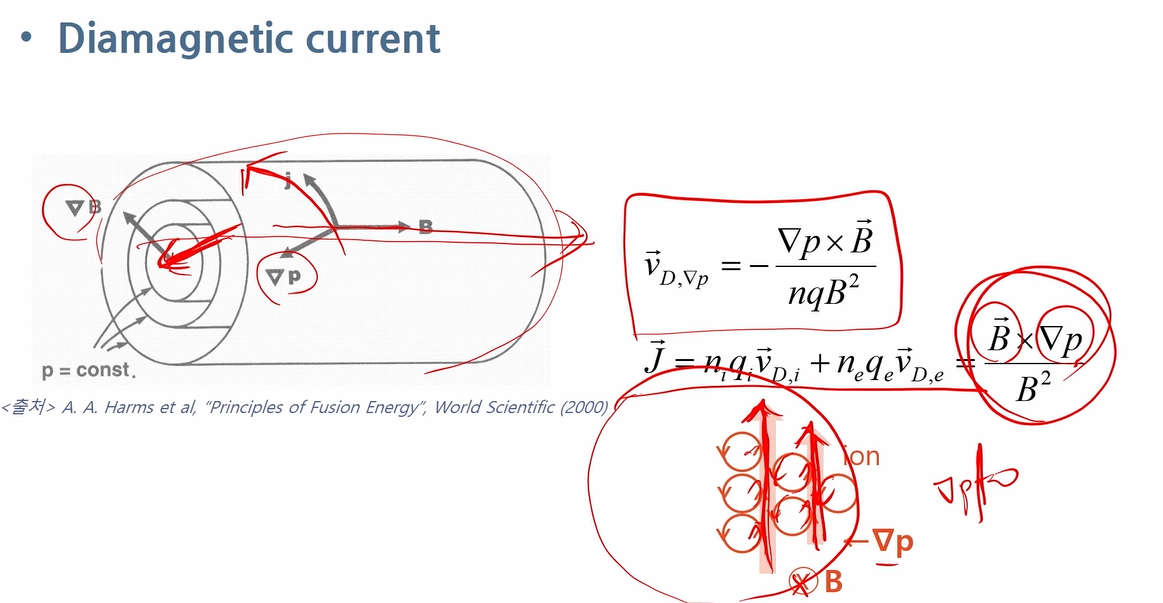
Diamagnetic current
- 자기장이 축 방향으로 걸려있고, 원통 내부로 갈수록 p가 증가한다.
- cation은 B의 왼손 감은 방향으로 원운동할 것이다.
- 그런데 grad p가 존재하므로 통 내부에서는 한쪽 방향으로 flow가 있는 것으로 보인다!
=> current를 계산가능.
- 이 현상은 net B를 감소시킨다.
- 과연 이 system에서 equilibrium이 만들어질 수 있는가?
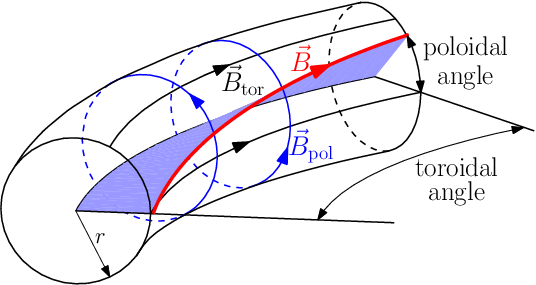

Beta
- 단위 자기압마다 얼마나 많은 플라즈마압을 건질 수 있는지의 척도
- Plasma beta, toroidal beta, poloidal beta, troyon beta 등의 beta가 쓰인다. (꼭 무언가를 써야한단건 없음)
- 대개 beta의 제곱은 fusion power에 비례한다.
Resistivity
- eta = m * v_e,i / (n * e^2)
- 이 값에 따라서 plasma의 안정성이 달라질 수 있다.
- 이 값은 MHD에서 유도될 수 있다.
Flux
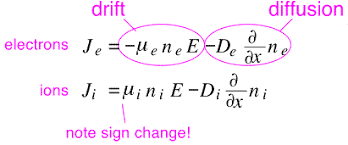

- flux의 식은 mobility와 diffusion coeffecient를 담고 있다.
- 각각 무슨 의미를 담고 있는가?

- 이것은 collision frequency의 목록인데 얘네들은 왜 도대체 저렇게 값을 달리하는가? (위 링크에 유도과정 있음)
- ee ie ei ii가 왜 다 다를까?
'[硏 Ⅰ] 연구하다 - 교양 > 시험 공부 전반' 카테고리의 다른 글
| 유체 (0) | 2021.09.15 |
|---|---|
| 핵융합 이론 정리 (3/4) (0) | 2021.08.15 |
| 핵융합 이론 정리 (2/4) (0) | 2021.08.14 |
| 최근 물리의 정석 고전역학편 읽으면서 새로 깨달은거 (0) | 2021.07.24 |
| 카테고리의 나눔, 향후 2주간의 계획 (0) | 2021.06.12 |


댓글