[검색해서 들어오신 분들께 : 이 글은 정보가 없습니다!]
다행히 토카막은 내용이 쉽다!
라고 생각하자 마자 뒷부분 내용 발작...

Tokamak
- closed magnetic confinement

- 토카막에는 토러스를 따라 도는 방향[toroidal]의 자기장이 걸린다.
- 토카막 도넛 내부에서는 자기장이 uniform하지 않고 도선 중심 거리에 반비례한다.
- 따라서 토러스의 가장 중심으로 향하는 grad B가 존재한다.
- 자기장이 꺾여있으므로 B의 curvature도 존재한다.
- 따라서 고려할 변수는 grad B에 의한 drift와 curvature에 의한 drift.

- 위의 두 drift에 의해 ion은 위로 올라가고 electron은 아래로 내려가게 된다. (charge separation)
- electric field의 생성.
- E cross B에 의한 drift가 토러스 바깥 방향으로 작용한다. 이때 e와 i가 받는 힘의 방향은 같은데, E에 의한 drift는 E cross B / B^2이기 때문이다.
- 이때 특별한 조치를 해주지 않아도 plasma current가 있을 수 있는데, 어떨까?
- charge separation이 있으므로 둘을 섞어주기 위해선 poloidal의 자기장을 걸어준다.
- B_poloidal은 어떻게 만들 것인가?
- 플라즈마 전류를 toroidal 방향으로 흘려주면 이것이 B_p를 만들겠구나.
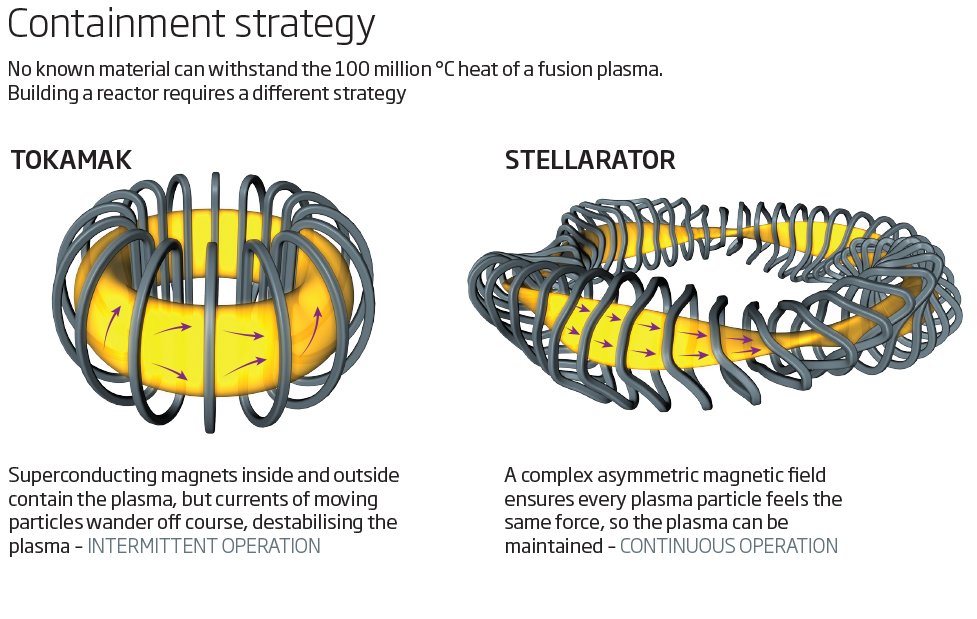
- 그렇게 플라즈마 전류를 흘리는 방식이 tokamak이다. (러시아 중심)
- 전류를 흘리는 대신 장치를 꼬아 만든 것이 stellarator이다. (미국 중심)

- 플라즈마에 전류는 어떻게 흘려보낼 것인가?
- Faraday's law : 멀리 떨어져있어도 전류의 공급 가능.
=> center solenoid, poloidal field coil(=equilibrium coil, vertical coil)
- 왜 옆에 coil을 설치하지 않고 tokamak torus hole 내부에 solenoid를 만들었는가?
- 토카막의 고유한 문제점 : center solenoid의 원리를 고려하면 전류를 반복적으로 넣어줘야하는데, 따라서 tokamak 내부의 plasma는 생겼다가 없어졌다를 반복한다. (pulsed operation)
- B_toroidal >> B_poloidal : torus를 크게 도는 helical magnetic field가 생성되는 이유.
- J_toroidal >> J_poloidal
- Open magnetic system에서는 얼마나 입자를 잃는데 시간이 빨리 걸리는가?
=> 그것이 정말로 우리가 closed magnetic confinement system에 의존해야만 하는 이유게 되는가?
JET 장치 :
- 플라스마는 어떻게 움직일까?
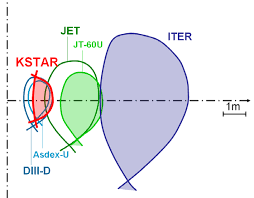
ITER 장치 :
- R0 = 6.2m. a = 2.0m로 상당히 크다.
- 2025년까지 1st plasma를 목표
KSTAR :
- 1.8m, 0.5m. 1억도 plasma를 만드는데 성공.
- ELM(edge-localized modes, 플라즈마 경계면 불안정 현상)를 오래동안 재현하는데 성공.
Tokamak Variables
- fusion reactor가 만족해야할 조건 : n * tau * T >= 3E21 m-3*s*KeV ~ 5 bar(~대기압)*s
- 보통 triple product는 잘 쓰지 않는다.
- n_e / n_GW(Greenwald)의 단위를 주로 쓴다.
- tau 대신 H_98, H_89를 쓰는 경우도 많다.
- n*T를 곱한 값(P와 비례)을 이야기하지 않고 보통 beta_N(normalized)에 대해 이야기한다.
Tokamak geometry
- R_0 : major radius
- a : minor radius
- Lamda = R_0/a : aspect ratio
- 이 값이 크면 둥글둥글한 토카막이 만들어진다. (spherical torus, 우리나라의 VEST tokamak 등)
- Epsilon = a/R_0 : inverse aspect ratio
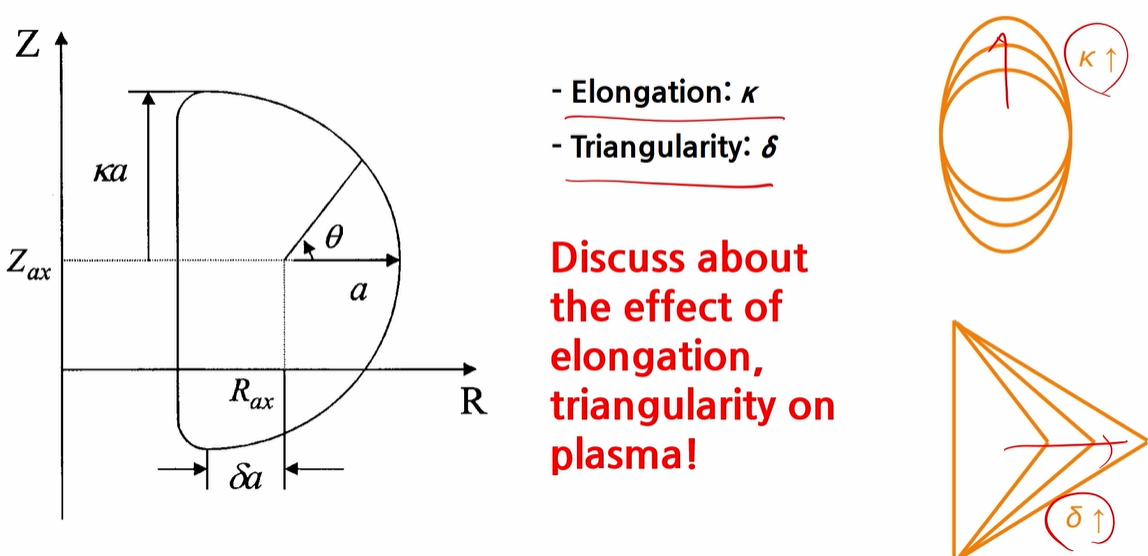
- kappa : elongation의 척도. k=1일 때 원. 커지면 위아래로 볼록한 타원에 가깝게
- delta a : 원래 원형에서 찌그러져 옆으로 퍼진 정도. delta는 triangularity(=삼각도).
- 위의 두개는 plasma의 형상과 관련된 것이다.
Beta
- beta_t = (plasma pressure) / (magnetic pressure = B_t^2/(2*mu0) )
- B_t는 R_0 거리 중심부의 값을 사용한다.
- beta_t = beta_normalized(beta_N) * (plasma current) / (a * B_t)
- beta_p = (plasma pressure) / (magnetic pressure = B_p^2/(2*mu0) )
- B_p는 중심으로부터 a거리 가장자리의 값을 사용한다.
Energy confinement time
- W(plasma energy) / ( P_in - partial dW/dt )
- plasma가 stable한 경우에는 partial dW/dt=0
- P_in은 J_p, B_t, n, R, a, k 등 수많은 실험변수들을 통해 data를 fitting한다.
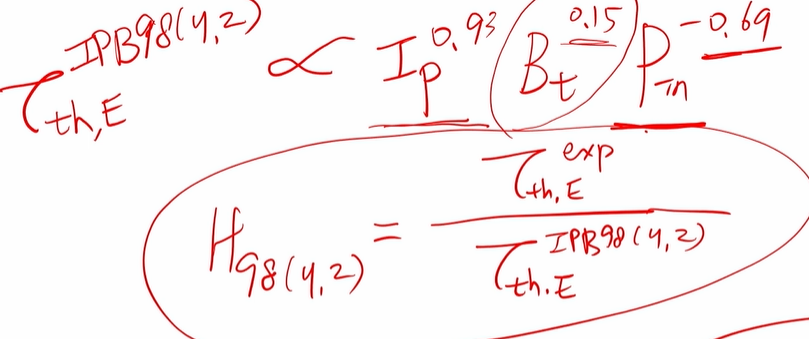
- thermal energy와 fast particle energy로 나뉘는데... thermal energy의 confinement time은 다음과 같이 나온다
- IPB98은 dataset의 이름이다. H-mode에서 얻어진 것이다.
- 이 값을 통해 H_98이 정의된다. 이 값이 1인 경우 IPB98과 동일한 confinement time이 얻어졌다는 뜻이다. 1보다 더 크면 그 기준 장치보다 성능이 더 좋았다는 것을 의미한다.
Greenwald density = n_GW = I_p / ( pi * a^2 )
- n_e가 저 값에 도달하면 plasma가 굉장히 불안해져서 disruption될 수 있다.
Iota = delta theta / ( delta phi / (2*pi) )
- toroidal 방향으로 한바퀴 돌았을 때 poloidal 방향으로 얼마나 가느냐?
- helice가 얼마나 꼬여있는지의 척도.
- 2*pi / iota = q = r/R * B_t/ B_p = safety factor. 플라즈마의 수송 등과 관련된다.
S (magnet sheer, 얼마나 꼬이는가) = r/q * dq/dr
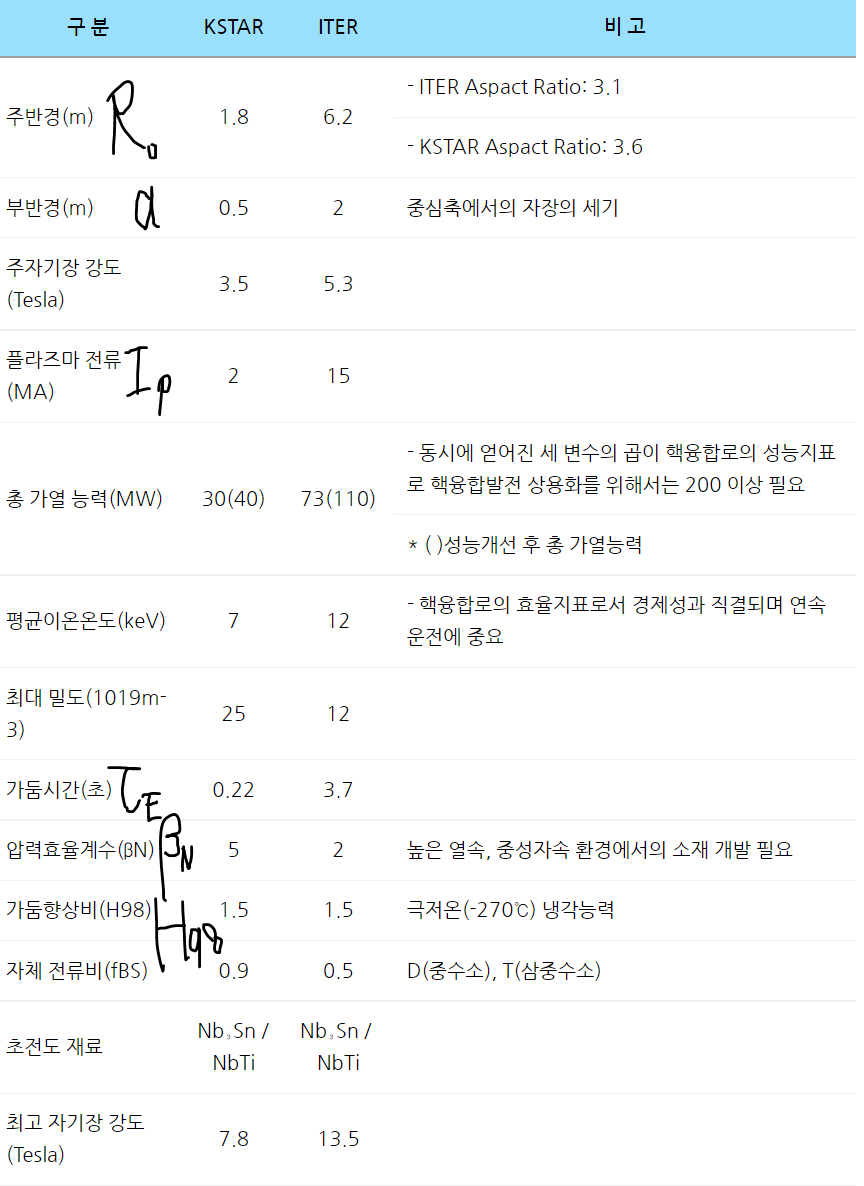
- 지금까지의 variable을 바탕으로 위 tokamak들의 성능을 이해할 수 있겠는가?
plasma에는 magnetie flux surface가 생긴다.
- p가 constant인 지점들이 나타난다. ( J cross B = grad P에서, J와 grad P, B와 grad P가 수직인 지점들)
Tokamak plasma equilibrium
- plasma의 equilibrium을 알기 위해 풀어야 하는 방정식 (ideal MHD에서 유도)
1. J cross B = grad P
2. curl B = mu0 * J
3. div B = 0

- Grad-Shafronov equation : thorus에 대해 위의 세 방정식을 연립해 풀이한 식.
- 비선형 편미분방정식이고, 주요 가정은 ideal MHD와 toroidal 축대칭.
- 유도 과정 간략하게 정리. 생략된 부분 많음

- F는 mu0 * I_p / 2pi

- J cross B = grad P 에서 J와 B를 p와 t 성분으로 모두 나누어 해결한다.
- grad p에 대한 위의 식은 ksi와 F에 대한 식으로 나오게 된다...
1. div B = 0을 통해 B_p를 얻는다
2. mu0 * J_p = (curl B)_p 를 통해 J_p와 B_t를 얻는다.
3. mu0 * J_t = (curl B)_t를 통해 J_t를 얻는다.
4. grad p의 식에 넣는다.
- del에 star가 붙은 기호는 elliptic operator
- Grad-Shafranov equation은 plasma의 equilibrium을 나타내고 있는 식인데, 무엇이 평형을 이루고 있는가?
- B_p가 작용하는 힘이 B_t의 힘 & 자기선속 위에서 plasma의 load와 평형을 이루어야 한다는 식이다.
- 이외에도 tokamak에 작용하는 힘 : a의 부피방향 이외에도 R방향으로 커지려는 힘이 존재한다.
1. Hoop force : B의 ds에 대한 선적분은 Ksi(flux)이므로 항상 일정해야만 한다. 그런데 바깥으로 갈수록 그 거리가 멀어지므로 자기장은 안쪽으로 올수록 커진다. 이로 인해 magnetic pressure는 증가한다. 따라서 torus 안쪽에서 바깥쪽으로 향하는 힘이 존재한다.
2. Tire tube force : 타이어를 위에서 누르고 뗄 때 튕기는 힘이 존재. (땅에 닿는 면적 << 바깥 면적) 따라서 바깥으로 튕겨나가려고 한다.
3. 1/R force : tokamak의 중심에서 멀어질수록 B는 거리에 반비례하여 줄어드는 경향으로 인해 중심부의 magnetic pressure가 더 크다. 따라서 바깥으로 향하는 힘이 존재한다.
=> 따라서 아래에서 위 방향으로 향하는 vertical field coil을 걸어줘야만 한다. 그러면 torus의 중심방향으로 작용하는 자기력으로 인해 equilibrium이 맞춰진다.
- radial 방향은 그렇게 equilibrium을 맞춰줄 수 있겠는데, 그렇다면 vertical 방향의 움직임은 어떻게 막을까?
Tokamak plasma instabilities
- stability : lineary stable, lineary unstable
- 약간의 Q(perturbation)을 주었을 때 복구될 수 있는가? : Q * exp(-iwt)에서 Im(w)의 부호가 stability를 결정
- Energy principle : delta W를 따지는 것.
- instability의 soruce : J 또는 grad p
Macroscopic
- Ideal, Restistive
1. Ideal : plasma의 resistivity가 없는 경우
- current-driven [kink] : internal, external
- external kink가 가장 중요. q_a[Kruskal-Shafranov criterion]를 1보다 크게 만들어야 한다.
- pressure-driven : interchange mode, ballooning mode
- interchange mode : 꼬인 자기장을 따라 입자가 움직이다 보면 입자가 내외부로 반복해 이동한다. 내부가 good curvature, 외부가 bad curvature가 된다. 바깥쪽이 perturbation이 자라기 쉽다.
- ballooning mode : 토러스 바깥 부분에서는 풍선이 커지듯이 플라즈마가 자랄 수 있다. 이를 해결하기 위해 beta-limit을 준다.
- vertical instability (VDE) = 위아래로 움직이는 plasma column이 벽을 때려 사라지는 현상. 이때 tokamak의 위에서 아래로 작용하는 curvature가 양인 자기장을 걸어주면 중심부로 작용하는 J cross B의 힘을 제공가능하다.
2. Resistive
- current-drive : Tearing mode(TH), Neoclassical Tearing mode(NT)

- resistive가 0인 경우 perturbation이 주어져도 flux surface들이 서로 만나는 일은 없다.
- 그렇지 않다면... flux surface가 만나는 현상이 발생하기도 한다. - magnetic island(자기 섬)
- TM (tearing mode) : dW/dt (delta'에 비례) 가 양수인 경우 발생한다. (시간에 따라 island가 커진다)
- delta prime은 tearing mode 전후의 ksi의 중심부거리 r에 대한 변화율의 차이이다. 양수인 경우 tearing mode가 발전하고 음수인 경우 neoclassical tearing mode가 발전할 가능성이 있다.
- 참고 : resistive=0인 경우 instability가 빠르게 발전하는데, 그렇지 않은 통상 경우 instability가 상대적으로 느리게 발전한다. 왜 이런가? (magnetic diffusion equation의 고려)
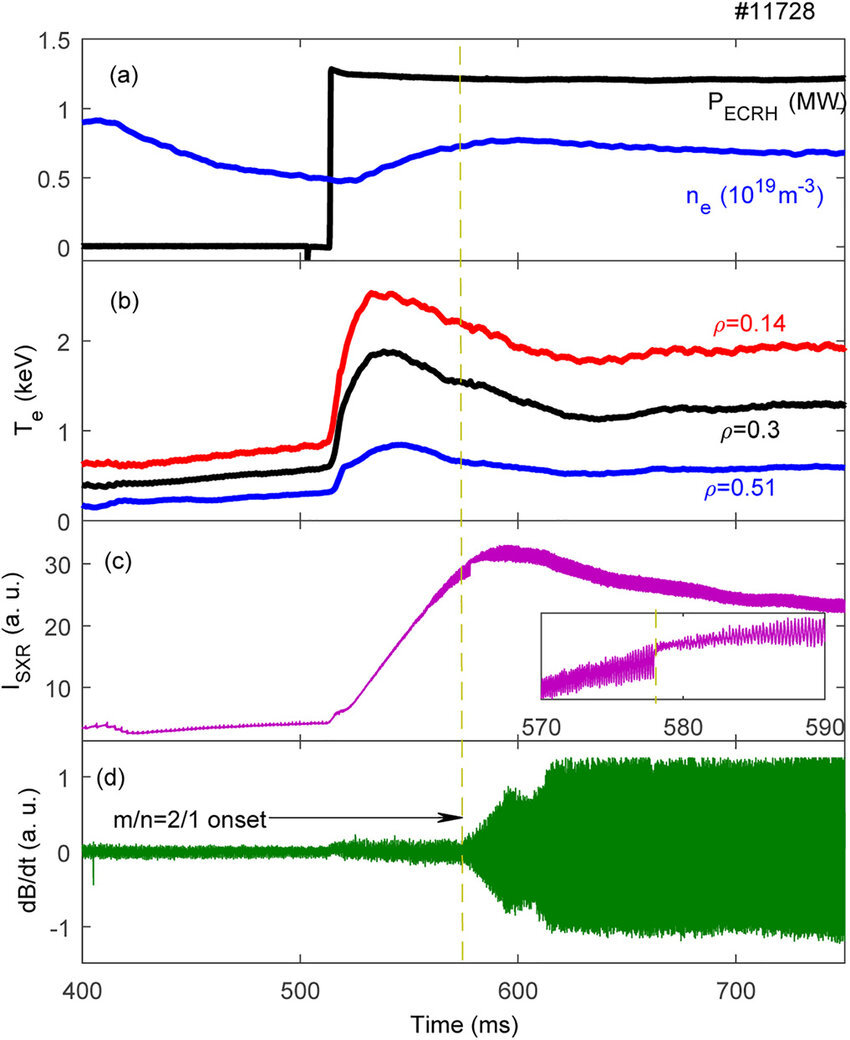
- NTM (neoclassical tearing mode) : delta'가 음수인 경우 자란다. beta_N이 증가하면 커진다.
- 시간에 따라 가열을 하게 되면 beta_N의 값은 증가한다. 도중 떨어지는 지점이 있는데 이때 B의 변화가 요동친다.
- island가 발생한 plasma가 poloidal 방향으로 순환할 때 고르지 않게 signal이 잡히는 것이다.
- 위 현상을 막기 위해 beta_N을 2 미만으로 두는 것을 목표로 한다.
- NTM이 발생한 영역의 변위-pressure의 그래프가 flat해진다. 그 옮긴 영역만큼의 에너지를 잃는다. 해당 구역에서 grad p=0이 되어버리는 것이므로 plasma가 만들어내는 자발전류는 0이 된다. 이것을 해결하기 위해서는 이 잃어버린 전류를 대신 공급하는 방법이 효과적이다.
- ECCD, ECH(heating만 해주는 것도 안정화가 가능) 방법 참고.
Microscopic
Turbulence : plasma transport와 관련된다.
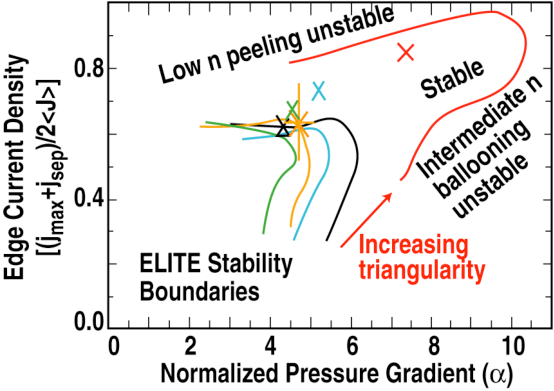
ELM 현상 : Edge localised mode : ideal의 current&pressure-driven이 섞인 형태.
- plasma의 가장자리에서는 current가 증가하고 pressure가 감소한다.
- grad p가 있으면 current가 증가하기 때문에 발생하는 현상.
- 왜 ELM을 control하는 것이 중요할까? (wiki에도 대충은 나와있지만, tokamak 벽의 손상을 야기할 수 있고 다른 instability를 trigger할 수 있기 때문...
- KSTAR에서는 외부에서 coil current를 올리면 그에 의한 자기장의 영향으로 ELM이 잠시 사라진다. (외부의 resonance magnetic perturbation으로 ELM을 제어)
- 다른 방법은 없나?
Peeling-balloonging mode.
Nonlinear instability : sawtooth, disruption(짧은 시간동안 플라즈마가 붕괴).
- sawtooth : center에서 시간에 따른 전자 중심부 온도를 관측한 결과 sawtooth와 같은 plot을 얻었다. (주기적)
- Kadomtsev : 가열을 해주면 중심부부터 온도가 오른다. 그렇게 되면 current가 오르고 q가 1 아래로 떨어지는데 이때 불안정성이 생긴다. 불안정성이 생기면 다시 T는 오르고 current가 떨어지고 q가 1 위로 오르고...의 진동을 반복한다.
- Neoclassic tearing mode를 유발한다.
- disruption : plasma의 에너지가 시간에 따라 떨어져 0이 된다. (thermal quench) 이때 plasma의 전류는 조금 뛴 후(spike : 이건 또 왜 발생하는가?) 크게 떨어진다. I_p가 0으로 되는 한편 기타 전자 - runaway electron에 의한 current quench가 발생한다.
- 짧은 시간동안 W와 I_p가 모두 소멸하는 현상. beta-limit에 도달하거나 density limit에 도달하거나, vertical displacement 등이 있을 때 발생하는 것으로 추정. 자세히는 모르는데, 아무튼 plasma에 매우 큰 영향을 미친다.
- 이 현상으로 벽에 주는 damage를 mitigation하는 방법론 : MGI(massive gas injection), killer pillet 투입. SPI(shattered pellet injection)
원론적으로 delta W >0일 경우 stable하다.
- delta W의 W는 W_F[플라즈마 에너지], W_S[플라즈마 표면 에너지], W_V[vaccum energy]
- 물리적으로 왜 이것이 양수일 때 안정한가?
참고 : plasma의 에너지 델타를 결정하는 식

Safety factor
- Kruskal-Shafranov criterion
- q_a = a * B_t / ( R_0 * B_p) = a * B_t / { R_0 * mu0 * I_plasma / (2pi * a) }
- 이 값은 또 B_t / I_plasma에 비례한다. 따라서 plasma current가 적고 toroidal 방향 자기장이 클수록 좋다.
Tokamak plasma transport
- plasma transport :
1. density gradient를 없애는 방향으로 flux : Gamma = - D * grad n
- diffusion coefficient : D ~ (delta x)^2 / (2*tau) ~ kai ~ a^2 / tau_E : 중요한 내용.
2. 온도 차이를 상쇄하는 방향으로 heat flux : q = -k * grad T
- k = n*kai
- 자기장을 거스르는 방향으로 diffusion이 발생. D_per = eta_per * n * sum(k*T) / B^2
: Kai_i ~ 40 Kai_e, ~ 10E-4 m2/s로 예측했었다.
- Bohm diffusion의 실험은 D_per = 1/16 * k*T_e / (e*B) : 그리고 다른 상수들도 매우 다른 값
: 실제로 Kai_i ~ Kai_e, ~ 1m2/s로 측정됨.
=> fully ionized with B : 이론과 실험이 매우 큰 괴리가 있음. 바나나를 고려해야한다. (물론 그렇게 시도한 neoclassical transport 이론에서도 tokamak의 현상을 잘 설명하지는 못했다...)
- collision이 증가함에 따라 중간에 D가 증가하지 않는 정체구간이 있다...
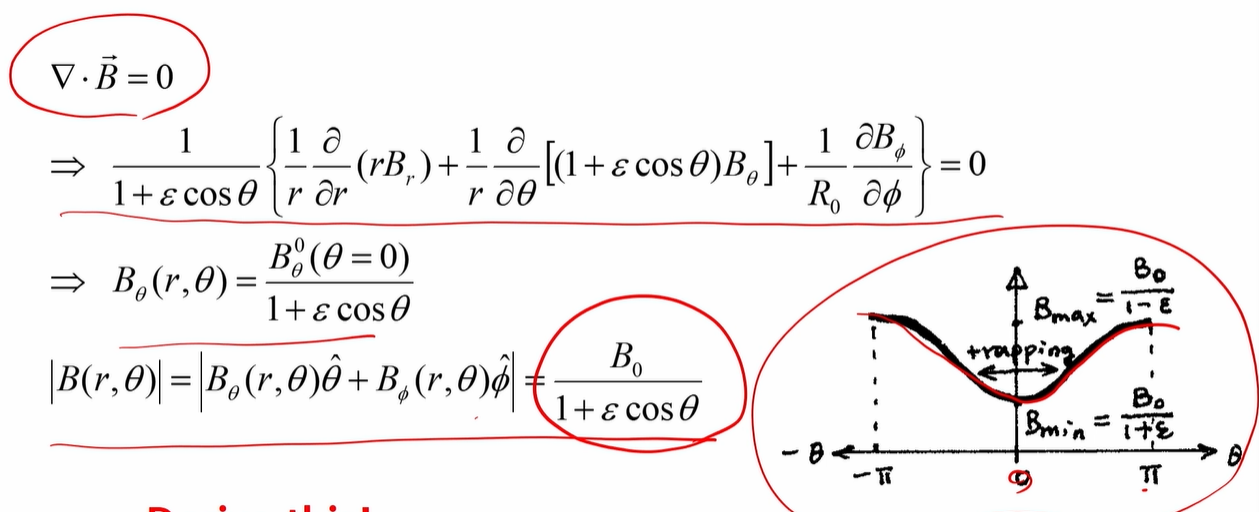
- tokamak은 단면에서 바깥으로 갈수록 B가 약하고 토러스 중앙을 향할수록 B가 강하다. abs(B) = B0 / (1+ epsilon * cos theta)
- 그래서 입자가 그 영역 사이에서 trapping된다.
=> neoclassical transport theory. [바나나 이론]
- B cross grad B의 방향이 위쪽이다. (= grad B에 의한 drift가 위쪽 방향)
- 그렇다 보니 flux가 banana 모양을 그린다. D는 banana의 width의 제곱에 비례하는 식으로 주어지게 된다.
Bootstrap current
- 입자가 가두어지는 banana는 바깥쪽에도 있고 안쪽에도 비슷한 수효만큼 있는데 안쪽에서 입자가 더 많이 발견된다...
- 아무튼 바나나 둘이 서로 상쇄가 되지 않는데, 그 사이로 current가 흐를 수 있다. (안쪽 전류의 방향이 우세), flow로 인한 momentum 생성.
- J_BS는 grad p에 비례한다.
- 이건 좋은 효과인가? 나쁜 효과인가?
- 복잡한 turbulance가 생기는 것 : eddy size = 1~2cm, lifetime = 0.5~1ms. : 실험값과 유사했다.
- neoclassical theory에서 할 수 없었던 것. turbulance로 diffusion 설명하기.
=> anomalous transport theory.
- 가열을 해주는 것과 T_i의 상승은 linear하지 않고, grad T / T가 const가 되는 느낌으로 되었다.
- profile consistency, profile stiffness, profile resilience라고 한다.
- T_i를 r에 대해 log scale로 그릴 경우 graph가 일정하게 올라가는데... linear scale일 때는 어떻게 상승할지?
- Microinstabilities에 대한 가설들이 등장. 기존 실험결과와 일반적이다.
- Two-stream/beam plasma instability : high energy beam이 들어왔을 경우 발생하는 불안정성
- drift(universal) instability : grad n, grad p가 wave를 만들어내는 것이 커지면서 instability로 발전.
- trapped ptl mode : banana trap과 위의 instability들과 상호작용해서 불안정성이 커지는 경우. TEM, TIM
=> 이것들이 turbulance를 만들어낸다. (r/a가 커질수록 n과 T의 fluctuation은 심해진다)
- instability는 어떻게 turbulance로 발전할까?
- H-mode의 발견, 1982 : r에 대한 grad p가 갑자기 오르는 현상. (댐과 같은 무언가가 생겨서 particle들이 바깥으로 나가는 것을 막는 현상. edge transport barrier. n_e barrier)
- H-mode에서 turbulence가 사라지고 grad T/ T가 const가 되는 현상이 상당부분 감소하였다.
- 1990년대 중반 : plasma 전류를 바꾸면 grad q=0인 부분 근처에서 T가 급격히 증가하는 현상. (T barrier)
: H-mode의 현상이 plasma 내부에 발생한 것. Internal transport barrier.
- Bootstrap current가 그 부분에 생기게 된다 : q의 안정화. 외부에서 넣어주는 전류가 없어도 non-inductive로 구동할 수 있게 되는 현상?
- I-mode, L-mode, H-mode는 어떻게 다를까...
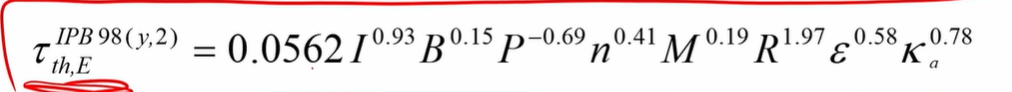
Energy confinement time : 대충 parameter로 fitting을 한다. IPB98은 위와 같다.

또 H-mode를 만들기 위한 power의 식은 저렇게 fitting되었다.
'[硏 Ⅰ] 연구하다 - 교양 > 시험 공부 전반' 카테고리의 다른 글
| 9/23 상담학 (0) | 2021.09.23 |
|---|---|
| 유체 (0) | 2021.09.15 |
| 핵융합 이론 정리 (2/4) (0) | 2021.08.14 |
| 핵융합 이론 정리 (1/4) (1) | 2021.08.13 |
| 최근 물리의 정석 고전역학편 읽으면서 새로 깨달은거 (0) | 2021.07.24 |



댓글